Le taux de croissance global mesure la variation de la valeur sur une période donnée, tandis que le taux de croissance annuel moyen est utilisé pour calculer le rythme moyen de variation d’une variable (PIB, inflation, etc.) sur une période donnée.
Calculer, lire et interpréter un taux de variation cumulé
le taux de variation cumulé mesure l’évolution d’une donnée sur plusieurs périodes. Il est calculé à partir des taux de variation de chacune des périodes.
A voir aussi : Tout savoir sur la mutuelle retraitée
Il n’est pas possible d’additionner les taux de variation. Il est donc nécessaire de transformer chaque taux de variation (TV) en coefficient multiplicateur !
Il suffit alors de multiplier ces coefficients multiplicateurs pour connaître le coefficient multiplicateur pour toute la période.
A lire également : Conditions d'éligibilité aux chèques-vacances pour retraités : critères essentiels
Ce multiplicateur peut ensuite être transformé en taux de variation.
Lecture du résultat : Le taux de variation cumulé se lit comme un taux de variation simple. Il est nécessaire d’indiquer s’il y a une augmentation ou une diminution et le résultat est lu en pourcentage.
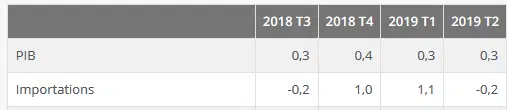
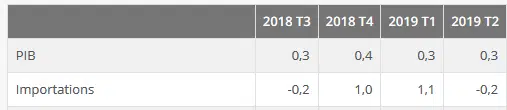
Application : Évolution en % du PIB et des importations de la France
- Transformez le taux de variation du PIB (T3 2018) en multiplicateur
Réponse 1.003 CM = (TV/100) 1.
ici CM = (0.3/100) 1
2. Calculez le multiplicateur qui permet de traduire la croissance du PIB de la France pour la période (du troisième trimestre 2018 au deuxième trimestre 2019).
Réponse Le PIB a été multiplié par 1,013. Pour répondre à cette question, il n’est pas possible d’additionner les différents taux de variation. Il est donc nécessaire de transformer chaque taux de variation en coefficient multiplicateur.
1,003* 1,004* 1,003* 1,003 = 1,013
3. Exprimez votre résultat en % de variation
AnswerPIB a augmenté de 1,3 % sur l’ensemble de la période (du troisième trimestre de 2018 au deuxième trimestre de 2019). Transformation du coefficient multiplicateur en taux de variation : (1,013 — 1) * 100 = 1,3 %.
4. Mesure (en %), l’évolution des importations au cours de la période (du troisième trimestre de 2018 au deuxième trimestre de 2019).
Réponse Les importations ont augmenté de 1,7 %. Rappel : Pour répondre à cette question, il n’est pas possible d’additionner les différents taux de variation. Il est donc nécessaire de transformer chaque taux de variation en coefficient multiplicateur.
0,998* 1,01* 1,011* 0,998 = 1,017
Une augmentation de (1,017-1) * 100 = 1,7 %
Taux de croissance annuel moyen
Le TCAM permet de savoir si la croissance a été forte ou non pendant une certaine période de temps et de la comparer à d’autres périodes qui peuvent être plus courtes (ou plus longues). Par exemple, dans le graphique 1, grâce au TCAM, nous constatons que la croissance a été beaucoup plus forte pendant les Glorious Thirty que dans les périodes suivantes. Le taux de croissance annuel moyen est donc un indicateur qui permet de comparer la croissance au cours de différentes périodes ou dans différents pays au cours de la même période.
Il s’agit donc d’une moyenne (géométrique) des différents taux de croissance de la période étudiée. Le taux de croissance annuel moyen facilite les comparaisons entre des périodes d’amplitude différente, ce qu’un taux de croissance global ne permet pas.
Source : profdeses.org
Questions :
- Quelle est l’utilité du TCAM ?
- Notez la formule de calcul du TCAM
- Notez la phrase de type à utiliser.
Interpréter un taux de croissance annuel moyen
Lors des tests du baccalauréat, vous n’aurez probablement pas à calculer un taux de croissance annuel moyen. Cependant, il est nécessaire que vous sachiez lire un TCAM et que vous soyez capable de faire une phrase pour le décrire. La phrase la plus simple est du type suivant :
Entre 1950 et 1975, le PIB a augmenté en moyenne de 5,3 % chaque année.
Conseil : Evitez les phrases telles que : « TCAM est de 5,3% », qui sont une pure paraphrase du document, et qui ne montrent pas que vous avez compris la notion de TCAM.
Source : INSEE
Question 1 : De combien de% a augmenté le PIB entre 1999 et 2009 ?
Réponsele PIB a augmenté de 14,9%. En effet, le pourcentage de variation = (Va-Vd) /Vd = (1960−1705,6) /1705 ,6 = 14,9 %.
Question 2 : Calculez maintenant l’importance de la croissance qui s’est produite, en moyenne, chaque année durant cette période.
Réponse : Le taux de croissance annuel moyen entre 1999 et 2009 a été de 1,4 %.
Question 3 : Écrivez une phrase qui donne le sens de ce résultat.
Réponse Cela signifie que le PIB a augmenté en moyenne chaque année en France de 1,4 % entre 1999 et 2009.
Exercice 2
Taux de croissance annuels moyens du commerce international et de la production mondiale, mesurés par le PIB mondial (en %)
| Périodes | Commerce international | Production mondiale |
| 1950-1960 | 6.3 | 4.2 |
| 1960-1970 | 8.3 | 5.3 |
| 1970-1980 | 5.2 | 3.6 |
| 1980-1990 | 3.7 | 2.8 |
| 1990-1996 | 5.9 | 1.4 |
| 1996-2000 | 8.2 | 3.4 |
| 2000-2005 | 4.5 | 2.0 |
Source : GATT, OMC, 2013
1) Que signifie les données en gras ?
Réponses-Elon, l’Organisation mondiale du commerce, chaque année, en moyenne, entre 1950 et 1960, le commerce international a augmenté de 6,3 %. Selon l’Organisation mondiale du commerce, chaque année, entre 1950 et 1960, la production mondiale a augmenté de 4,2 % en moyenne.
2) Sachant que le TCAC du commerce mondial était de 6,3 % entre 1950 et 1960, dans quelle mesure le commerce mondial a-t-il augmenté pendant cette période (en d’autres termes, calculer le taux de croissance global durant cette période) ? Et une production mondiale ?
Rappel de réponse : Il n’est pas possible d’ajouter (ou de multiplier) des taux de variation. Il faut transformer chaque taux de variation en coefficients multiplicateurs ! Pendant 10 ans en moyenne, le commerce mondial a augmenté de 6,3 %, c’est-à-dire qu’il a été multiplié par 1,063 x 1,063… x 1,063 pour 10 fois, soit 1,063 10 ≈ 1,84
Le commerce mondial a augmenté de 84 % de 1950 à 1960
Pendant une moyenne de 10 ans, la production mondiale a augmenté de 4,2%, c’est-à-dire qu’elle a été multipliée par 1,042 x 1,042… x 1,042 pour 10 fois, soit 1,042 10 ≈ 1,51
La production mondiale a augmenté de 51 % entre 1950 et 1960.
3) Quelle est l’idée principale du document ?
Réponse : Le rythme de croissance du commerce international est toujours supérieur à celui de la production mondiale.
